Fractals
Introduction
My interest with fractals started in 2017 when I was staying with my grandparents, and found an old book of fractals. Finding Daniel Shiffman’s Nature of Code website and The Coding Train YouTube channel soon after prompted me to start writing my own fractal renderers. This post will be a lightning fast review of these renderers and other related experiments.
Early Fractal Renderers


My very first attempt used C# and .NET libraries, and was as clunky as it could possibly have been. I then moved onto the more suitable Processing library for Java that I continued to use for many other projects. The Processing version of the renderer could be navigated naturally using the mouse, and had optimizations like increasing the number of iterations (i.e. accuracy of the fractal’s shape) with the level of zoom.
Other Fractals
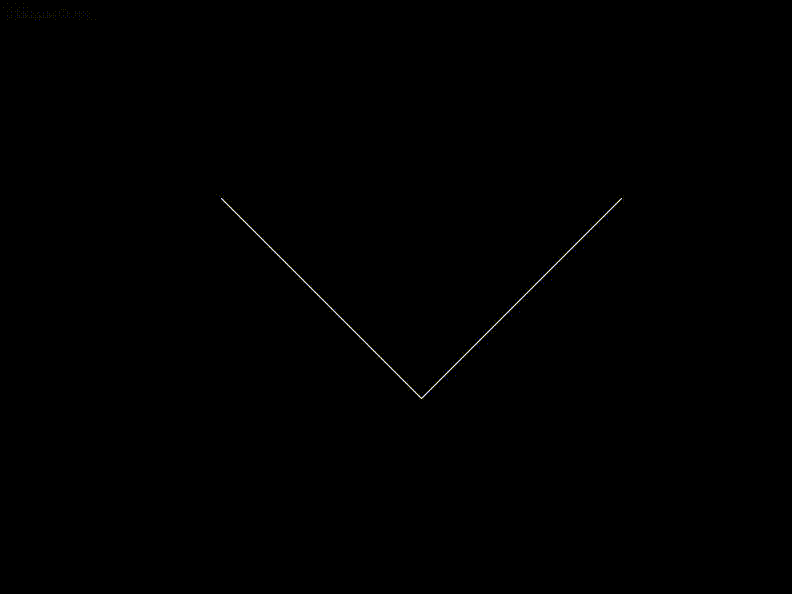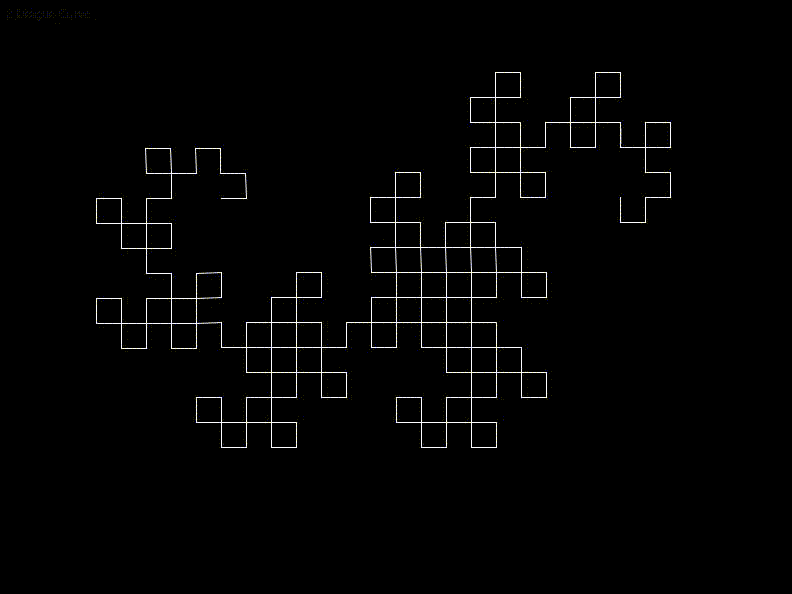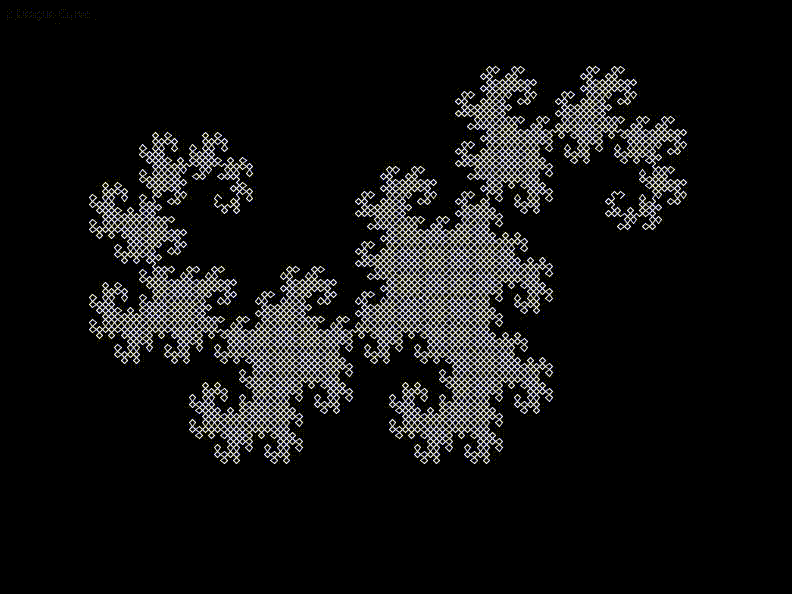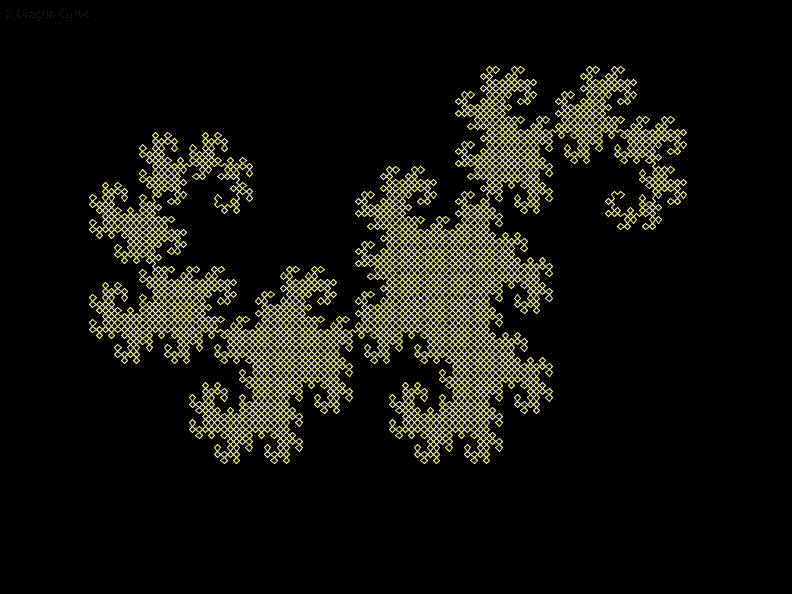





I came across Lindenmayer Systems and generated a number of different fractals using a basic stack based approach. I also tried rendering the basic Menger Sponge and Inverted Menger Sponge 3D fractals.
I was interested upon revisiting L-Systems to read about their place in the family of formal grammars and variations upon the original formulation. I might explore these further soon.
Better Renderers
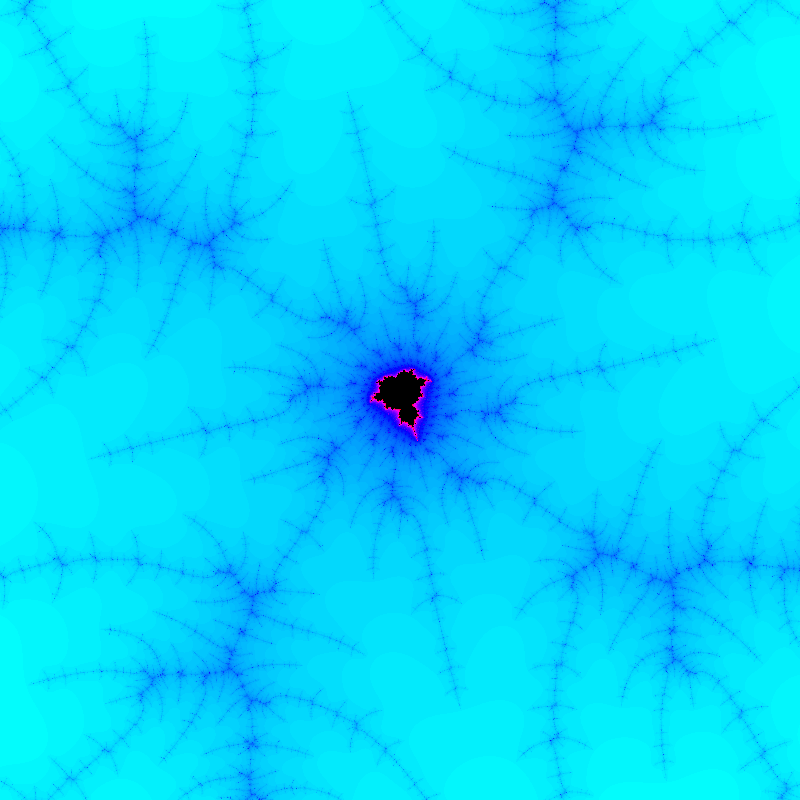

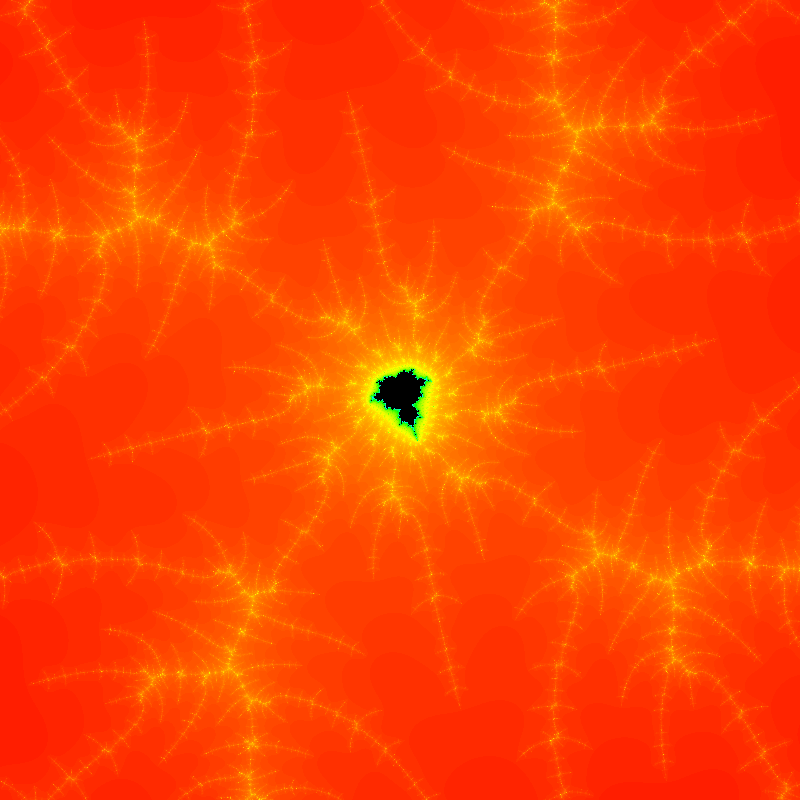
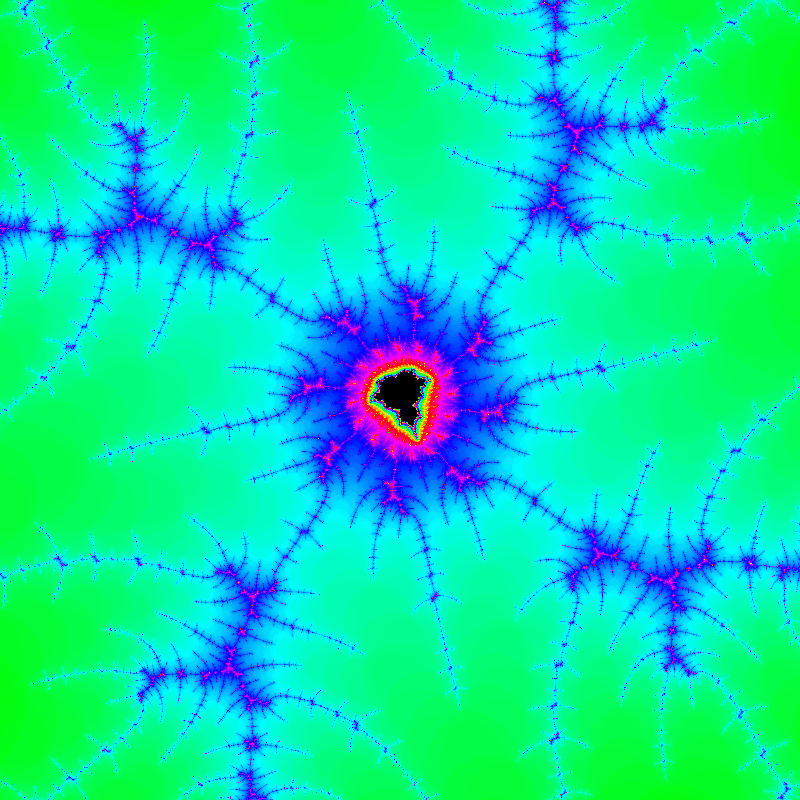

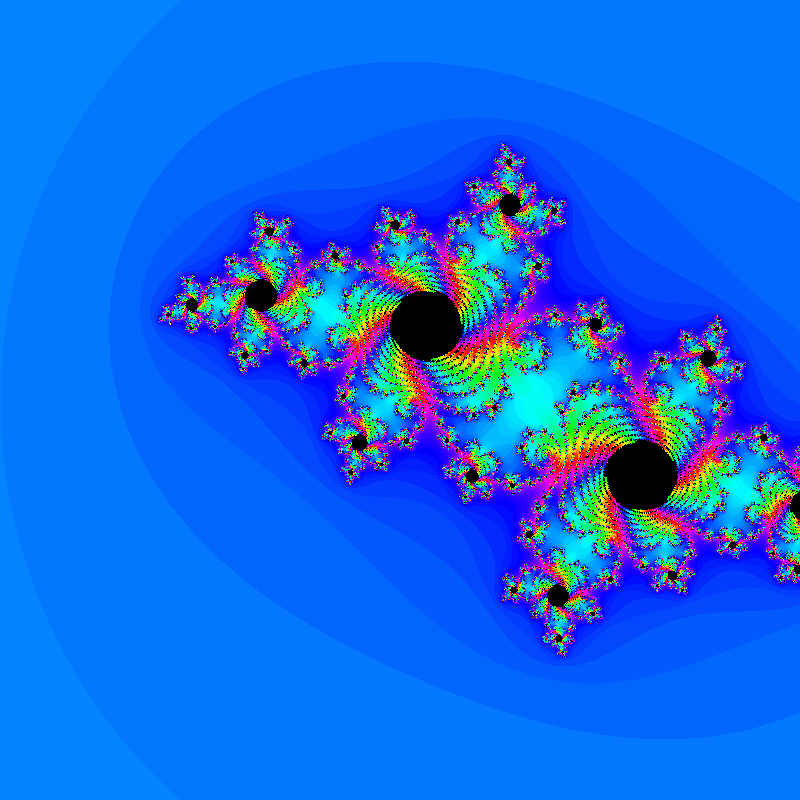

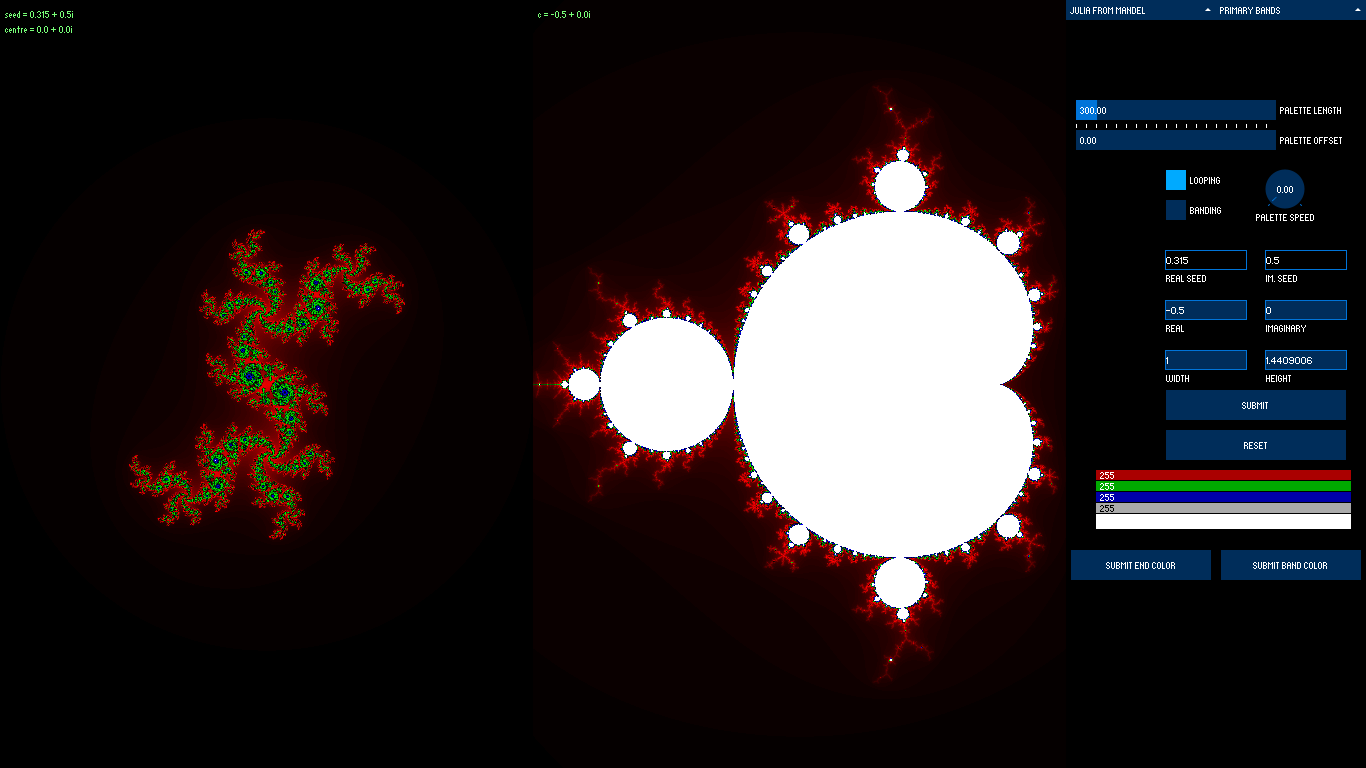
My next fractal project evolved into my project for A-Level Computing coursework. This is the most fully featured renderer I’ve made so far. It could render the Mandelbrot set and the Burning Ship Fractal, as well as the Julia sets that correspond to each point of those sets. It also had:
- GUI
- Two Rendering Windows
- 3 Levels of Detail
- Multithreaded Rendering
- Multiple Colour Palettes
- Looping Colour Palettes


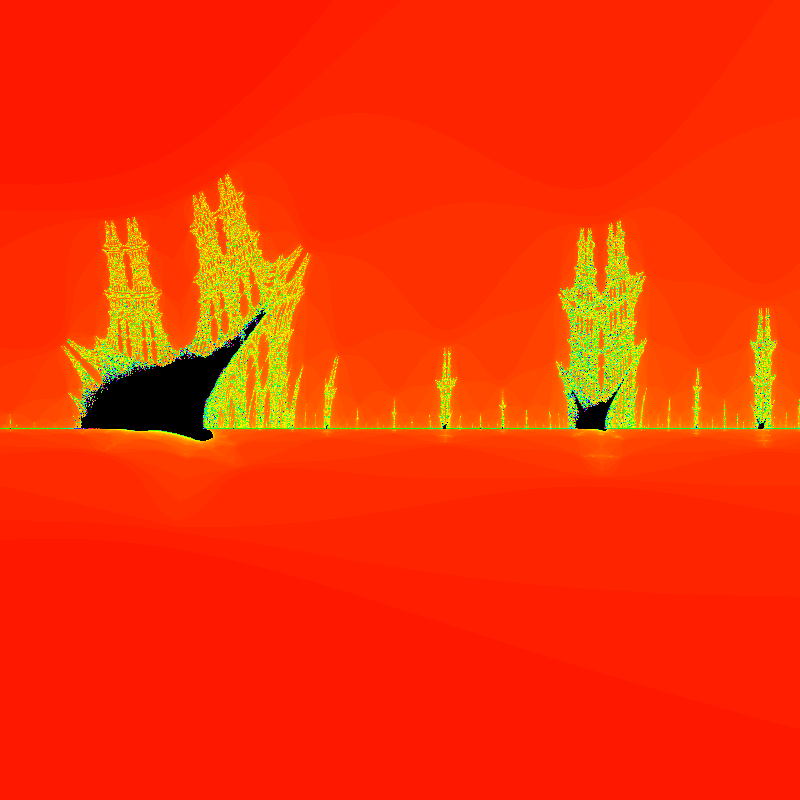
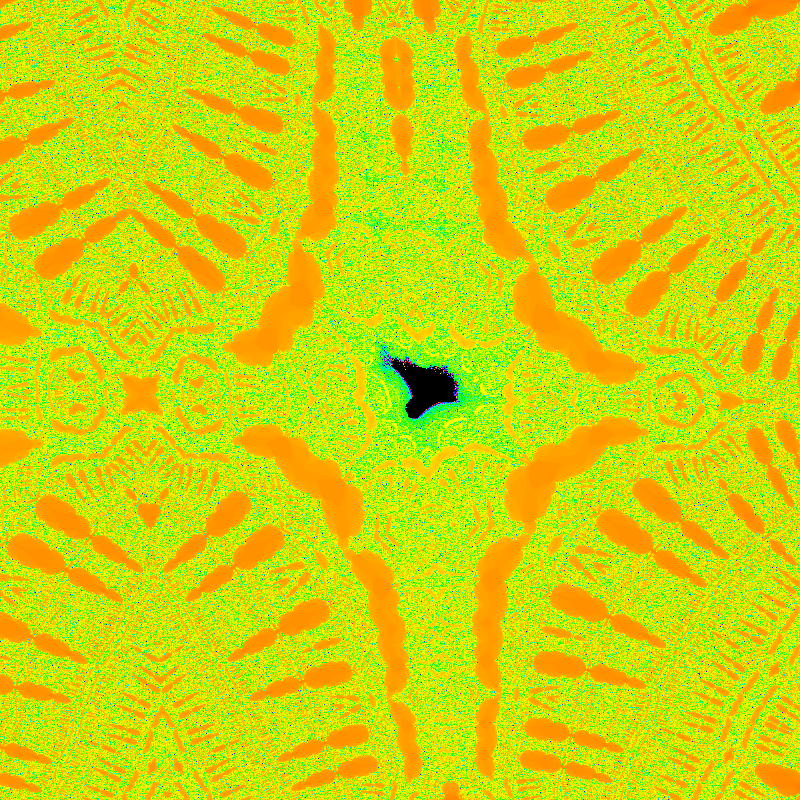

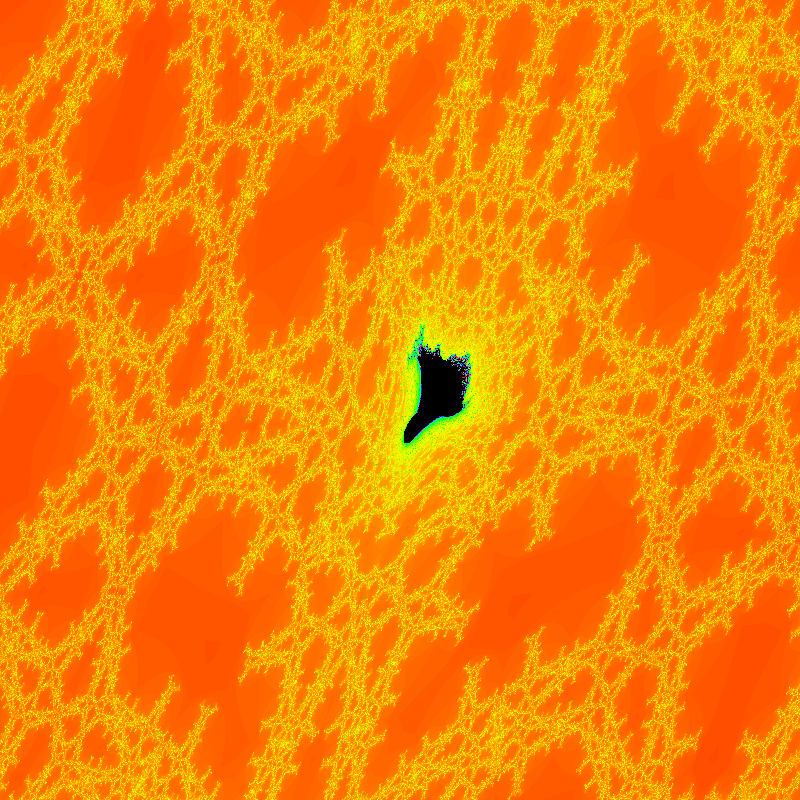


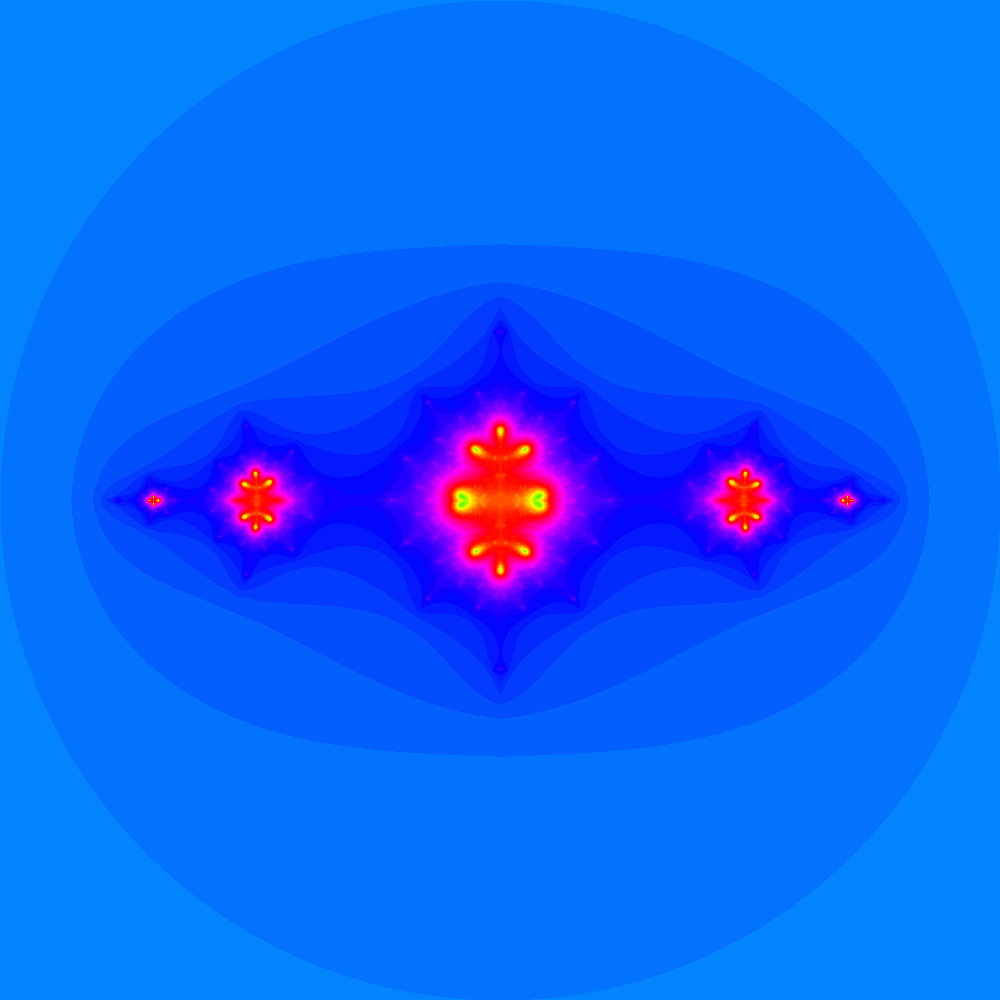
Other Escape Time Fractals
There are fractals generated in the same fashion as the Mandelbrot set but with different equations.
| Fractal Name | Equation |
|---|---|
| Mandelbrot Set | z = z^2 + c |
| Burning Ship Fractal | z = abs(z)^2+c |
| Multibrot Set | z = z^d + c |
| “Burning” Multibrot | z = abs(z)^d+c |






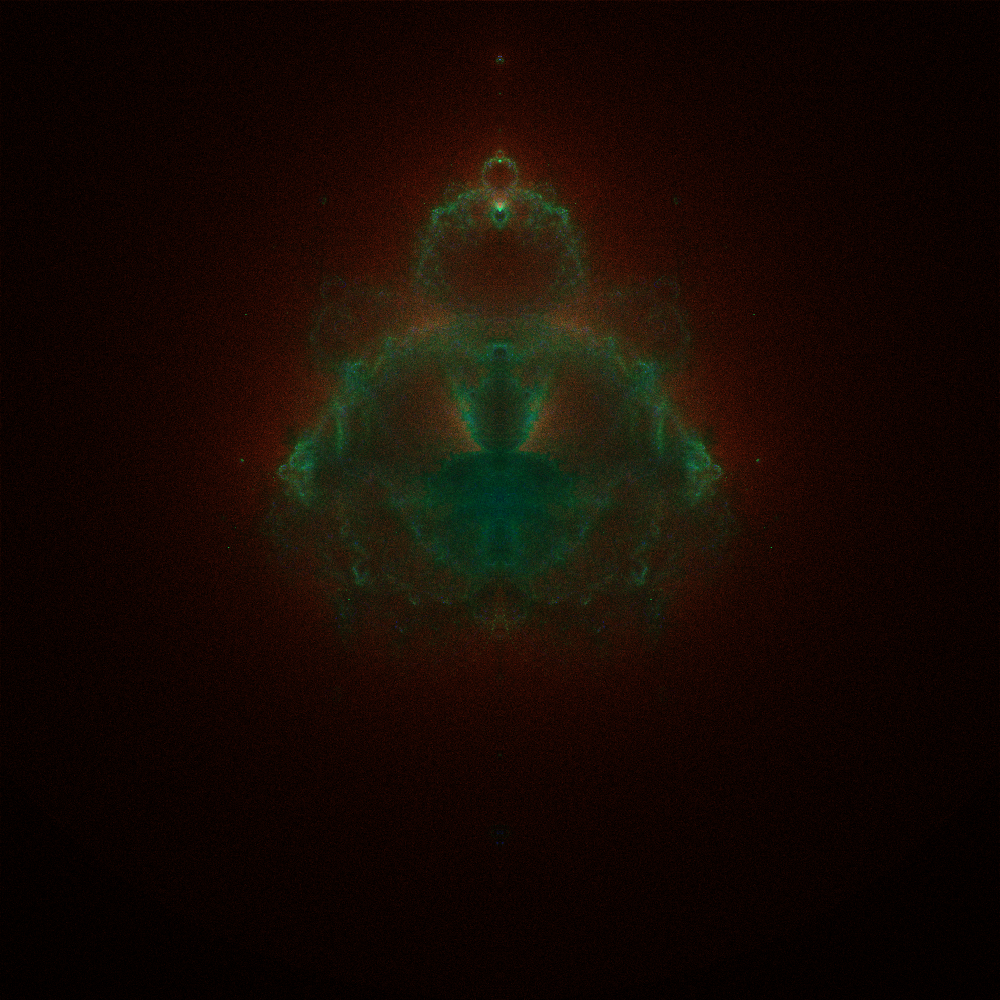
Buddhabrot
A different method of rendering the Mandelbrot set that I want to explore further in the future. In this method, pixels are coloured based on the frequency of that pixel’s location being “visited” by the iteration of a random sample of points in the complex plane. Only points that escape to infinity (hence are not in the Mandelbrot set) contribute to the frequency counts.

Next Projects
I’m keen to explore using shaders to exploit parrallel computation and improve the render speed, and signed distance fields (SDFs) for 3D or higher dimensional fractals in my next project. Inigo Quilez has some fantastic resources about SDFs and their uses.
